2. 中国食品药品检定研究院, 北京 100050
2. National Institutes for Food and Drug Control, Beijing 100050, China
单因素方差解析是常见的一种对连续数据的方差解析方法,其中应用最广泛的是多组数据的差异显著性检验,以此找出组间差异。然而,除上述应用外,日常工作中还经常遇到下述情况:1)在药品检测实验室,对方法精密度的计算和评价[1-3];2)能力验证提供者(proficiency testing provider,PTP)进行的所供样品均匀性评价和能力评定标准的计算[4];3)标准物质提供者(reference material provider, RMP)进行协作标定中的对照品的赋值等工作[5]。这些工作都离不开对试验所测数据的方差解析,求出其中所需的表达参数。
在计算上述各种目的所需指标时,需要有周密而完善的实验设计。一个切实可行的实验设计,不仅可以有效排除偶然因素造成的变异性,使实验误差降到最低限度,从而使所获结果更可靠,而且还可以节省人力、时间,降低实验成本,达到高效的实验目的[6]。目前,在进行上述实验或评价中,常见的问题是手工计算繁琐、实验设计不规范、对所需计算的方差成分不了解,从而导致许多困惑。
本文拟利用单因素多水平随机效应模型的实验设计,形成一个通用模板,对上述情形所需的参数(指标)通过方差解析的方式进行计算演示,以便当遇到上述情况时,便于读者理解和科学、快速地计算所需指标。
1 单因素多水平随机效应模型的方差分析及其具体应用方差解析目的就是探讨不同因素、不同水平之间效应的差异。根据研究因素个数的不同,方差解析可以分为单因素方差解析、双因素方差解析等。实验设计中只有一个因素取不同的水平进行试验,而其他因素保持不变,这样的试验称为单因素试验(one factor trial),相应的方差解析就是单因素的方差解析。根据因素水平的选择,方差解析的模型又可分为固定效应模型(fixed-effects model)、随机效应模型(random-effects model)和混合效应模型(mixed-effects model)。若是固定几个水平进行试验并加以比较,属于固定效应模型;若从所有水平中随机抽取几个水平进行试验并加以比较,从而检测所有水平的差异,属于随机效应模型;两者的混合则属于混合效应模型[7]。
随机效应模型的实验设计是经典线性模型设计的一种推广,就是把原各固定效应因素视为来自总体的随机效应因素,而在原来各因素的记录数据或观测(如重复次数或多时间点的记录)间建立起一定的相关性模型。如在对样品均匀性分析时,将各支样品视为总体中随机选取的样品,代表总体信息;将参与检测的实验室,视为从总体检测实验室中随机抽取的实验室;将各种检测药品视为总体药品中的一部分等等。该模型可用来拟合非独立观测的数据,具有计算简便、能选择相关的预测参数(predictors)、对因素的压缩程度较小等优点。
本研究探讨的是采用单因素多水平随机效应的实验设计模型。详见表 1。
|
|
表 1 单因素多水平随机效应试验模型 |
假设因素有j个水平,j=1, 2, 3, …, c,在每个水平j下进行i次独立重复,i=1, 2, 3, …, r,得到的试验结果为xj, 1, xj, 2, ..., xj, r, 试验结果服从正态分布N(μj,σ2); 应特别指出在每个水平下重复次数r=2时,其计算形式较重复次数r≥3有一定的区别,详见“3.2”节的讨论。
实验的总样本数[7]为n=cr。
因素在j水平下观测值的样本均值,即组内均值xj:
| $ {{\bar x}_{\rm{j}}} = _{\rm{r}}^1\sum\limits_{i = 1}^r {{x_{{\rm{ij}}}}}, ~~{\rm{j}} = 1, 2, 3, \cdots, {\rm{c}} $ | (1) |
样本的总均值:
| $ \overline{ \overline x} = \frac{1}{{{\rm{cr}}}}\sum\limits_{i = 1}^r {\sum\limits_{j = 1}^c {{x_{{\rm{ij}}}}} }, ~~{\rm{j}} = 1, 2, 3, \cdots, {\rm{c}}, ~~{\rm{i}} = 1, 2, 3, \cdots, {\rm{r}} $ | (2) |
总离差平方和SST,描述了所有观察效应之间的差异。
| $ S{S_{\rm{T}}} = {\sum\limits_{i = 1}^{\rm{r}} {\sum\limits_{j = 1}^{\rm{c}} {\left( {{x_{{\rm{ij}}}}-\overline{ \overline x}} \right)} ^2} } $ | (3) |
| $ S{S_{\rm{T}}} = S{S_{\rm{A}}} + S{S_{\rm{E}}} $ |
组内离差平方和SSE反映了各组内部因重复性实验而产生的随机抽样误差。
| $ S{S_{\rm{E}}} = {\sum\limits_{i = 1}^{\rm{r}} {\sum\limits_{j = 1}^{\rm{c}} {\left( {{x_{{\rm{ij}}}}-{{\bar x}_{\rm{j}}}} \right)}^2 } } $ | (4) |
组间离差平方SSA主要反映了各组样本均值间的差异,既包括了随机抽样误差,也包括不同的实验室所造成的系统误差。
| $ S{S_{\rm{A}}} = \sum\limits_{j = 1}^{\rm{c}} {r{{\left( {{\overline {{x_{\rm{j}}}} }-\overline{ \overline x}} \right)}^2}} $ | (5) |
总离差平方和的自由度;组内离差平方和的自由度;组间离均差平方和的自由度;由此得组
| $ 内均方M{S_{\rm{E}}} = \frac{{S{S_{\rm{E}}}}}{{cr-c}} = \frac{1}{{cr-c}}\sum\limits_{i = 1}^r {\sum\limits_{j = 1}^c {{{\left( {{x_{{\rm{ij}}}}-{\overline {{x_{\rm{j}}}} }} \right)}^2}} } : $ | (6) |
| $ 组间均方:M{S_{\rm{A}}} = \frac{{S{S_{\rm{A}}}}}{{c-1}} = \frac{1}{{c-1}}\sum\limits_{j = 1}^c {r{{\left( {{\overline {{x_{\rm{j}}}} }-\overline{ \overline x}} \right)}^2}} $ | (7) |
| $ 组内方差分量\left( {{S_{\rm{r}}}} \right):{S_{\rm{r}}} = \sqrt {M{S_{\rm{E}}}} $ | (8) |
| $ 组内方差分量\left( {{S_{\rm{L}}}} \right):{S_{\rm{L}}} = \sqrt {\frac{{M{S_{\rm{A}}}-M{S_{\rm{E}}}}}{r}} $ | (9) |
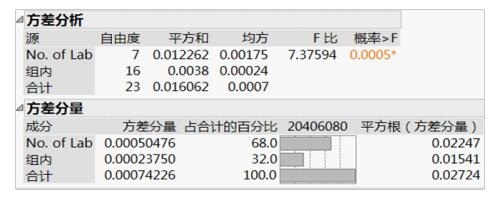
上述的单因素方差解析过程均可由软件(如Excel、SAS和JMP等)计算汇总得“方差分析表”,如图 1。
|
图 1 方差分析表 |
上述设计和相应的方差计算,对药品检测实验室中常见的分析方法精密度计算、实验室检测能力评价、样本均匀性评估以及标准品协作标定的赋值等具有很好的应用价值。这四方面所需的参数,均可由此单因素的方差解析获得MSE和MSA,然后根据每个试验目的进行进一步的运算。
1.1 应用于确定分析方法的精密度计算在确定分析方法的精密度试验中,如果表 1中因素所涉及的不同水平是同一个实验室中不同的分析人员、不同的设备等的组合条件,则此试验的目的是为获得分析方法的重复性标准差和中间精密度IP(标准差);如果表 1中因素所涉及的不同水平是不同实验室、不同天数和不同分析人员等的组合条件,则此试验模型的目的是为获得重复性标准差和再现性标准差。
| $ \begin{array}{l} {{\hat \sigma }_{{\rm{IP}}}}或{{\hat \sigma }_{{\rm{Rep}}}} = \sqrt {{S_{\rm{L}}} + {S_{\rm{r}}}} = \sqrt {\frac{{M{S_{\rm{A}}}-M{S_{\rm{E}}}}}{r} + M{S_{\rm{E}}}} \\ \;\;\;\;\;\;\;\;\;\;\;\; = \sqrt {\frac{1}{r}M{S_{\rm{A}}} + \left( {\frac{{r-1}}{r}} \right)M{S_{\rm{E}}}} \end{array} $ | (10) |
重复性标准差的计算公式:
| $ {{\hat \sigma }_{\rm{r}}} = {S_{\rm{r}}} = \sqrt {M{S_{\rm{E}}}} $ | (11) |
在进行实验室能力评定或标准物质标定过程中,所使用的试验样品均应满足均匀性这一前提条件。样品间的标准差,亦即组间标准差SL,与能力评定的标准差只要满足下式[4]就表明样本是均匀的:
| $ {S_{\rm{L}}} \le 0.3{{\hat \sigma }_{{\rm{PT}}}} $ | (12) |
对样品间标准差的计算一般按照下列规则进行:由主实验室制备并且包装一轮能力验证的样品或待标标准品的样品,然后独自或指定一个实验室进行均匀性的检验。实验时,从本批总体中随机选择c份,即在此试验中的因素为随机样本,从每个样品中制备r个独立测试份量,整个测量在独立重复性条件下完成。
| $ {S_{\rm{L}}} = \sqrt {\frac{{M{S_{\rm{A}}}-M{S_{\rm{E}}}}}{r}} $ | (13) |
实验室能力评定实验中所使用的试验样本均匀、稳定,实验室使用已标准化的测量方法,并且该方法的重复性和再现性可获得时,能力评定的标准差也可由上述的单因素方差解析进一步求算获得。
能力评定标准差的计算[4]:
| $ {{\hat \sigma }_{{\rm{PT}}}} = \sqrt {\frac{{M{S_{\rm{A}}}-M{S_{\rm{E}}}}}{r} + \frac{{M{S_{\rm{E}}}}}{r}} = \sqrt {\frac{{M{S_{\rm{A}}}}}{r}} $ | (14) |
协作标定(Collaborative Calibration)是指在多个具有同等能力的实验室间,使用法定方法进行测量,各实验室所得的实验数据按统计程序处理后得到标准物质的特性值[5]
所测样品的总均值:
| $ \overline{ \overline x} = \frac{1}{{{\rm{cr}}}}\sum\limits_{i = 1}^r {\sum\limits_{j = 1}^c {{x_{{\rm{ij}}}}} }, ~~{\rm{j}} = 1, 2, 3, \cdots, {\rm{c}}, \;\;{\rm{i}} = 1, 2, 3, \cdots, {\rm{r}} $ |
标准不确定度
| $ \begin{array}{l} {\mu _{\mathop {\left( {\rm{x}} \right)}\limits^ = }} = \sqrt {\frac{{S_{\rm{L}}^2}}{c} + \frac{{S_{\rm{r}}^2}}{{cr}}} = \sqrt {\frac{{rS_{\rm{L}}^2}}{{cr}} + \frac{{S_{\rm{r}}^2}}{{cr}}} = \sqrt {\frac{{rS_{\rm{L}}^2 + S_{\rm{r}}^2}}{{cr}}} \\ \;\;\;\;\;\; = \sqrt {\frac{{\frac{{M{S_{\rm{A}}}-M{S_{\rm{E}}}}}{r} + M{S_{\rm{E}}}}}{{cr}}} = \sqrt {\frac{{M{S_{\rm{A}}}}}{{cr}}} \end{array} $ |
| $ 即:{\mu _{\mathop {\left( {\rm{x}} \right)}\limits^ = }} = \sqrt {\frac{{M{S_{\rm{A}}}}}{{cr}}} $ | (15) |
置信区间:
根据表 1的单因素多水平随机效应的实验设计,我们将假定获得的检测数据汇总于表 2中。
|
|
表 2 原始数据汇总表 |
通过统计软件(这里使用JMP软件)对表 2进行数据的方差解析可得图 1的方差分析表。
由表 2可知r=3, c=8, n=24。
由图 1确定SSA、SSE和SST的自由度分别为dfA=7、dfE=16和dfT=23。
离均差平方和分别为SSA=0.012262、SSE=0.0038和SST =0.016062。
均方分别为MSA=0.00175、MSE=0.00024。
下面将以此实例作为上述四类试验的试验结果,对于不同实验类型所需参数进行计算演示。
2.1 分析方法精密度试验中的重复性标准差和中间精密度或再现性标准差计算假定欲对某一实验方法的精密度进行评价。如果表 2中的检测结果是在同一实验室中,使用同一样品(均质),采用不同分析人员、或不同仪器等组合为8个条件,每个条件下对样本重复测定3次所获得的数据,即可求出方法的重复性标准差和中间精密度;如果表 2中的数据是采用8个实验室对同一样品进行检测,每个实验室重复测定3次,即可获得方法的重复性标准差和再现性标准差。计算结果如下:
根据公式10,中间精密度或再现性标准差:
| $ \begin{array}{l} {{\hat \sigma }_{{\rm{IP}}}}/{{\hat \sigma }_{{\rm{Rep}}}} = \sqrt {\frac{{M{S_{\rm{A}}}-M{S_{\rm{E}}}}}{r} + M{S_{\rm{E}}}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sqrt {\frac{{0.00175-0.00024}}{3} + 0.00024} = 0.02714 \end{array} $ |
根据公式11,重复性标准差:
| $ {{\hat \sigma }_{\rm{r}}} = {S_{\rm{r}}} = \sqrt {M{S_{\rm{E}}}} = \sqrt {0.00024} = 0.01541 $ |
假定表 2的原始数据是对在实验室能力评定或标准物质标定中制备的样品进行的均匀性研究结果,即在同一个实验室中,从包装好的样本中随机选择8份,每一份样本制备3个测定份量所测得的原始数据。
根据公式13,样本间标准差:
| $ {S_{\rm{L}}} = \sqrt {\frac{{M{S_{\rm{A}}}-M{S_{\rm{E}}}}}{r}} = \sqrt {\frac{{0.00175-0.00024}}{3}} = 0.02247 $ |
根据公式11,样品内变异相当于重复性标准差:
将SL与能力评定标准进行比较即可判断该批制备的样品是否具有均匀性。
2.3 实验室能力评定标准差的计算假定表 2的原始数据是经过8个经验实验室对某一产品(已通过均匀性、稳定性评估)采用同一方法测得的原始数据,那么,可以使用这些数据求出作为能力评定标准的标准差。
根据公式14,能力评定标准差:
| $ \hat \sigma = \sqrt {\frac{{M{S_{\rm{A}}}}}{r}} = \sqrt {\frac{{0.00175}}{3}} = 0.00805 $ |
假定表 2的原始数据是协作标定的结果,即筛选出8个具有同等能力的实验室,每个实验室均采用规定方法,重复测定3次试验数据。
则标准物质的均值根据公式2得:
| $ \overline{ \overline x} = \frac{1}{{cr}}\sum\limits_{i = 1}^r {\sum\limits_{j = 1}^c {{x_{{\rm{ij}}}}} } = 0.68875 $ |
根据公式15,其标准不确定度:
| $ {\mu _{\mathop {\left( {\rm{x}} \right)}\limits^ = }} = \sqrt {\frac{{M{S_{\rm{A}}}}}{{rc}}} = \sqrt {\frac{{0.00175}}{{24}}} = 0.00854 $ |
置信区间:
| $ \begin{array}{l} \overline{ \overline x} \pm {t_{1-\alpha :c-1}}\sqrt {\frac{{M{S_{\rm{A}}}}}{{cr}}} = 0.68875 \pm 2.3646 \times \sqrt {\frac{{0.00175}}{{24}}} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = 0.68875 \pm 2.3646 \times 0.00854\\ \overline{ \overline x} \pm {t_{1-\alpha :c - 1}}\sqrt {\frac{{M{S_{\rm{A}}}}}{{cr}}} = 0.68875 \pm 0.02019 \approx 0.69 \pm 0.02 \end{array} $ |
1)本文给出的方差解析及各种计算,需要有严格的实验设计和数据探测,并保证其数据的独立性、正态性(离群值检查或对数据进行转换)和方差齐性这些前提。本实例是一个数据集完整的嵌套式随机效应的单因素方差解析特例。当数据集不完全符合表 1的结构,导致数据结构不均衡时,公式更复杂[7],这时,最好直接使用专业统计软件,计算出组内和组间的方差分量(如图 1中的下半部分);有些需使用其他计算方法,如标准物质的合并计算,需要使用权重法等[8]。
2)如若所建立的模型中在每个水平的试验重复测定次数仅为r=2时,一般使用极差法[2],即:
| $ MS_{\rm{E}}' = \frac{{\sum\limits_{j = 1}^c {S_{\rm{j}}^{'2}} }}{c} = \frac{{\sum\limits_{j = 1}^c {w_{\rm{j}}^2} }}{{2c}}\;\;\;\;\;r = 2 $ | (16) |
| $ M{S_{\rm{E}}} = \frac{{\sum\limits_{j = 1}^c {S_{\rm{j}}^2} }}{c} = \frac{{\sum\limits_{i = 1}^r {\sum\limits_{j = 1}^c {{{\left( {{x_{{\rm{ij}}}}-\overline {{x_{\rm{j}}}} } \right)}^2}} } }}{{c\left( {r-1} \right)}}\;\;r \ge 3 $ | (17) |
3)在实际应用中,对于四类分析应就具体的试验要求进行实验设计。研究表明[9],增加实验组数(c)比增加每组的重复次数(r)可更大地增加所得参数的稳健性或效能。本文的主要目的是拟通过一个适用于四类试验的模型,建立一个通用的计算模式,在实例分析中没有考虑到具体应用中因素水平的个数(c)以及在每个水平下的重复测定次数(r)。实际实施过程中,由于受现实条件(如成本)限制,需特别权衡成本与结果可靠性问题。一般应结合具体法规和实验的变异大小进行考虑,并尽可能地根据实验设计要求,增加实验组数。如对参加实验室能力认证的独立样本数c≥10,每个样本重复数r≥2次。
本文通过建立一个适用于上述四类分析的通用性实验设计,即单因素多水平随机效应模型的实验设计,利用JMP统计软件对该类型数据进行方差解析,将原本复杂的方差分析过程简化为方差分析表,并进一步结合具体应用中的方差成分需求进行计算演示,使药品检测实验室的分析人员能够用最短的时间快速理解,并系统掌握获得稳健可靠的所需参数,为今后在药品检测实验室开展相应的工作提供了很好的参考依据。
| [1] |
USP40-NF35: < 1010> Analytical Data-Interpretation and Treatment[S]. 2017.
|
| [2] |
ISO 5725-2: 1994 Accuracy (Trueness and Precision) of Measurement Methods and Results-Part2: Basic Method for The Determination of Repeatability and Reproducibility of a Standard Measurement Method[S]. 1994.
|
| [3] |
中国药典: 四部[S]. 2015, 附录9101: 374-377.
|
| [4] |
GB/T 28043-2011/ISO 13528: 2005利用实验室间比对进行能力验证的统计方法[S]. 2011.
|
| [5] |
ISO guide 35: Reference Materials-General and Statistical Principles for Certification[S]. 2006.
|
| [6] |
谭德讲, 马双成. 药品监督与检定中的统计学应用[M]. 北京: 中国科学技术出版社, 2011: 235-236.
|
| [7] |
高祖新. 医药数理统计方法[M]. 第五版. 北京: 人民卫生出版社, 1987: 186-189.
|
| [8] |
cdUSP40-NF35: < 111> Design and Analysis of Biological Assays[S]. 2017.
|
| [9] |
USP PF 40(5): < 1210> Statistical Tools for Procedure Validation[EB/OL]. [2017-07-29]. http://www.usppf.com/pf/pub/index.html.
|
 2018, Vol. 32
2018, Vol. 32 
