2. 北京市食品药品监督管理局, 北京 100053
2. Beijing Food and Drug Administration, Bejing 100053, China
为确保进口药品质量,《进口药品管理办法》 [1]规定,进口药品必须经口岸药品检验所(以下简称口岸所)进行检验,合格后方可进口[2]。北京市药品检验所(以下简称北京药检所)作为口岸所之一,承担着北京口岸进口药品的法定检验工作,检验数量呈逐年上升趋势。随着国家对药品监管力度的加强[3],除进口法定检验外,国家评价性抽验、市级监督性抽验、注册复核检验等各类检验任务也在逐年增加,因此充分利用已有数据,通过科学的数据预测方法,为检验业务管理工作提供支持、为领导决策提供依据[4-5],具有非常重要的现实意义。目前,时间序列模型的数据预测分析在环境、价格、消费等领域的应用非常广泛:例如张琼[6]对工程建设中主要材料价格波动情况进行的三次指数平滑预测,结果准确性较高;刘红梅等[7]对韶山红色旅游景区客源进行的灰色模型预测,是在建模的基础上进行适当原始数据预处理,可使预测结果的可信度提高;龚国勇[8]利用ARIMA模型对深圳GDP进行了预测,得到了较好的结果;杜家龙[9]利用一元回归多项组合方法、王莎莎等[10]利用组合预测模型,对国内生产总值(GDP)进行预测,等等。本文参考相关文献,基于北京市药检所2000-2015年的历史进口检品数据,采用ARIMA模型预测方法、三次指数平滑预测法、灰色模型预测法以及一元线性回归组合预测法对历史检品数量进行预测,并与实际数量进行比较以评价预测方法的适用性。结果表明:ARIMA模型预测方法相比其他3种方法,其准确度相对较高。本文采用ARIMA模型预测方法对2016年-2018年进口检品数量进行了预测。
1 预测模型选择常见的预测方法有二次移动平滑法、三次指数平滑法[11]、Winters加法[12]、Winters乘法、灰色模型法[13]、线性回归法[14]、ARIMA法[15]等等,各种预测方法在不同领域都会存在一些不足,例如拟合度差、精度不高、误差大等。而组合预测能够达到综合的、最有效的预测结果,更有效地改善模型的拟合能力并且提高预测精度[16]。
1.1 三次指数平滑预测法三次指数平滑是指数平滑法中的一种预测方法,相比一次、二次指数平滑法其能够跟踪时序的非线性变化趋势。任一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均。当时间序列观察值发展趋势单纯围绕某一水平做随机跳动时可以建立平滑模型:设时间序列为x1,x2,x3,…,第n+1期的一次平滑值为x'n+1,第n+1期的二次平滑值为x''n+1,第n+1期的三次平滑值为x'''n+1, xn+1为第n+1期的实际值,α为平滑系数在0~1之间。
| $ {{x'}_{n + 1}} = \alpha {x_{n + 1}} + \left( {1 - \alpha } \right){{x'}_{n + 1}} $ | (1.1) |
| $ {{x''}_{n + 1}} = \alpha {{x'}_{n + 1}} + \left( {1 - \alpha } \right){{x''}_{n + 1}} $ | (1.2) |
| $ {{x'''}_{n + 1}} = \alpha {{x''}_{n + 1}} + \left( {1 - \alpha } \right){{x'''}_{n + 1}} $ | (1.3) |
即:下一时期的预测值与上一时期的观测值和预测值有关。离预测期越远的观测值对预测值的影响越小。影响权重以指数形式递减。建立三次平滑预测公式:m为预测时段长度,an、bn、cn为预测模型中的平滑系数,y'n+m为n+m时段的预测值。初始值选择,可选择前几个观察值的平均值或取实际数据的初值[17]。本文选择的是取实际数据的初值,即2000年的值。
| $ {{y'}_{n + m}} = {a_n} + {b_n}m + {c_n}{m^2} $ | (1.4) |
| $ {a_n} = 3{{x'}_n} - 3{{x''}_n} + {{x'''}_n} $ | (1.5) |
| $ {b_n} = \frac{\alpha }{{2{{\left( {1 - \alpha } \right)}^2}}}\left[ {\left( {6 - 5\alpha } \right){{x'}_n} - \left( {10 - 8\alpha } \right){{x''}_n} + \left( {4 - 3\alpha } \right){{x'''}_n}} \right] $ | (1.6) |
| $ {c_n} = \frac{\alpha }{{2{{\left( {1 - \alpha } \right)}^2}}}\left( {{{x'}_n} - 2{{x''}_n} + {{x'''}_n}} \right) $ | (1.7) |
在灰色系统预测领域中,最为常见、应用也较广泛的是GM(1, 1)模型,1个变量,1阶方程,实际上是生成数列模型。所需样本数据比较少,计算起来比较简便,步骤是首先将无规律的原始数据进行累加,弱化了部分随机干扰或噪音后重新建模,再次对新得到的数据进行处理,便可以对处理后的模型进行预测。
给定原始数据列:
| $ {x^{\left( 0 \right)}} = \left\{ {{x^{\left( 0 \right)}}\left( 1 \right),{x^{\left( 0 \right)}}\left( 2 \right), \cdots ,{x^{\left( 0 \right)}}\left( n \right)} \right\} $ | (1.8) |
其中,上标0表示x(0)为原始数列,有n个观测值,对一次累加后,生成为:
| $ {x^{\left( 1 \right)}} = \left\{ {{x^{\left( 1 \right)}}\left( 1 \right),{x^{\left( 1 \right)}}\left( 2 \right), \cdots ,{x^{\left( 1 \right)}}\left( n \right)} \right\} $ | (1.9) |
其中,上标1表示新生成数列,同样有n个数值。设x(1)满足一阶线性微分方程:
| $ \frac{{d{x^{\left( 1 \right)}}}}{{dt}} = {\rm{a}}{x^{\left( 1 \right)}} = {\rm{u}} $ | (1.10) |
记参数列A为:
| $ {\rm{A}} = \left( {{\rm{a,u}}} \right) $ | (1.11) |
a为一阶线性微分方程(1.10)的发展系数,反映的是数列x(0)、x(1)的发展趋势;u为一阶线性微分方程(1.10)的协调系数,反映的是数据间的变化。根据最小二乘法对A进行求解,如下:
| $ {\rm{A}} = {\left( {{B^T}B} \right)^{ - 1}}{B^T}{Y_{\rm{n}}} $ | (1.12) |
其中:
| $ {\rm{B}} = \left\{ {\begin{array}{*{20}{c}} { - \frac{1}{2}\left[ {{x^{\left( 1 \right)}}\left( 1 \right) + {x^{\left( 1 \right)}}\left( 2 \right)} \right]}&1\\ { - \frac{1}{2}\left[ {{x^{\left( 1 \right)}}\left( 2 \right) + {x^{\left( 1 \right)}}\left( 3 \right)} \right]}&1\\ {}&1\\ {}&1\\ {}&1\\ { - \frac{1}{2}\left[ {{x^{\left( 1 \right)}}\left( {n - 1} \right) + {x^{\left( 1 \right)}}\left( n \right)} \right]}&1 \end{array}} \right\} $ | (1.13) |
| $ {Y_n} = {\left[ {{x^{\left( 0 \right)}}\left( 2 \right),{x^{\left( 0 \right)}}\left( 3 \right), \cdots ,{x^{\left( 0 \right)}}\left( n \right)} \right]^T} $ | (1.14) |
将a、u代入(1.15)中,因x(0)(1)=x(1)(1),得到下式:
| $ {{\hat {\bar X}}^{\left( 1 \right)}}\left( {k + 1} \right) = \left[ {{x^{\left( 0 \right)}}\left( 1 \right) - \frac{{\rm{u}}}{{\rm{a}}}} \right]{e^{ - ak}} + \frac{{\rm{u}}}{{\rm{a}}},{\rm{k}} = 0, \cdots ,{\rm{n}} $ | (1.15) |
| $ {{\hat {\bar X}}^{\left( 0 \right)}}\left( {k + 1} \right) = {{\hat {\bar X}}^{\left( 1 \right)}}\left( {k + 1} \right) - {{\hat {\bar X}}^{\left( 1 \right)}}\left( k \right) $ | (1.16) |
一元线性回归就是实际中的配直线问题。设x为自变量,y为因变量,选取n个样本值,作一条回归直线:
| $ {y_i} = {a_i} + {b_i}{x_i}\;\;\;\;\left( {i = 1 \cdots 5} \right) $ | (1.17) |
yi为各单个品种所对应组成的一元线性回归总检品数量的预测值,用标准估计误差ei求其组合预测的权重值wi,其预测模型:
| $ {w_i} = \frac{{\frac{1}{{{e_i}}}}}{{\sum {\frac{1}{{{e_i}}}} }} $ | (1.18) |
| $ {\rm{组合预测模型}}:y = \sum {{y_i}{w_i}} $ | (1.19) |
ARIMA模型的形式:考虑序列yt,若其能通过d次差分后变为平稳序列,即yt~I(d),则
| $ {u_t} = {\Delta ^d}{y_{\rm{t}}} = {\left( {1 - {\rm{B}}} \right)^d}{y_{\rm{t}}} $ | (1.20) |
ut为平稳序列,即ut~I(0),于是建立ARIMA(p,q)模型:
| $ {u_t} = c + {\mathit{\Phi }_1}{u_{t - 1}} + \cdots + \mathit{\Phi }{u_{t - p}} + {\varepsilon _t} + {{\rm{ \mathsf{ θ} }}_1}{\varepsilon _{t - 1}} + \cdots + {{\rm{ \mathsf{ θ} }}_q}{\varepsilon _{t - q}} $ | (1.21) |
经d阶差分后的ARIMA (p, q)模型称为ARIMA(p, d, q)模型,其中p为自回归模型的阶数,q为移动平均的阶数,εt为一个白噪声过程。有时为消除序列的异方差,需要对数据进行处理,一般情况下取其对数。ARIMA的思路很简单,首先用差分去掉季节性波动,并去掉长期趋势,然后平滑序列,用一个线性函数加白噪声的形式拟合序列,就是不断地用前p个值来计算下一个值。
2 进口检品数量的预测 2.1 历史数据预处理进口检品数量趋势不仅考虑以年递增的纵向趋势,还要考虑具有主要影响的单个品种数量的横向影响。在对历史数据进行提炼时,发现大约有28个品种的进口数量对总检品数量具有影响,使用SPSS软件进行相关性分析,相关系数达到0.9以上的有5个品种,分别用A、B、C、D、E表示,详细数据见表 1。
|
|
表 1 2000年-2015年的总进口检品数及具有主要影响的单个检品数 |
模型参数可以用Excel、SPSS、Matlab等软件来实现。
2.2.1 三次指数平滑预测初始值为2000年的值1783,根据数据趋势α=0.3[18],用Excel利用公式(1.1)(1.2)(1.3)作出一次指数平滑值、二次指数平滑值、三次指数平滑值[19],利用公式(1.5)(1.6)(1.7)作出平滑系数:
a2010=13758.51、b2010=2211.451、c2010=88.62657,
a2011=16212.6、b2011=2442.501、c2011=91.79113,
a2012=20456.48、b2012=3223.268、c2012=126.9196,
a2013=22144.67、b2013=2896.549、c2013=92.76916。
其三次指数平滑预测模型:
| $ {{y'}_{2010 + {\rm{m}}}} = {13758.51_{2010}} + {2211.451_{2010}}m + {88.62657_{2010}}{m^2} $ |
| $ {{y'}_{2011 + {\rm{m}}}} = {16212.6_{2011}} + {2442.501_{2011}}m + {91.79113_{2011}}{m^2} $ |
| $ {{y'}_{2012 + {\rm{m}}}} = {20456.48_{2012}}{3223.268_{2012}}m + {126.9196_{2011}}{m^2} $ |
也可以用SPSS20.0作出三次指数平滑的预测。
2.2.2 灰色模型预测利用Matlab软件对原始数据进行一次累加,生成累加矩阵,利用最小二乘准则计算待定参数的值。确定参数估计a=-0.23,u=1191.4,用excel通过(1.15)(1.16)公式进行预测计算。Matlab的a,u参数源代码:
clear
syms a u;c=[a u]';
A=[1783,2096,2449,2699,3209,4434,4953,6967,9851,13303,13111];
Ago=cumsum(A);n=length(A);for i=1:(n-1)
C(i)=(Ago(i)+Ago(i+1))/2;end
Yn=A;Yn(1)=[];Yn=Yn';E=[-C; ones(1, n-1)];
c=inv(E*E')*E*Yn;c=c';a=c(1);u=c(2);
a, u
2.2.3 一元线性回归组合预测将表 1中相关系数大于0.9的5个品种作为自变量,A为x1,B为x2,C为x3,D为x4,E为x5,总检品数量作为因变量作一元线性回归,用SPSS求出各系数,其一元线性回归方程:
| $ {y_\mathit{1}} = 1.655{x_1} + 9201.242 $ |
| $ {y_\mathit{2}} = 4.961{x_2} + 2047.83 $ |
| $ {y_\mathit{3}} = 18.749{x_3} + 7432.293 $ |
| $ {y_\mathit{4}} = 117.654{x_4} + 920.29 $ |
| $ {y_\mathit{5}} = 34.411{x_5} + 11361.164 $ |
根据上述方程及组合公式(1.18)(1.19)计算预测出相对误差较小的预测值,详见表 2。权重分别为w1=0.24,w2=0.38,w3=0.16,w4=0.11,w5=0.11。
|
|
表 2 单个品种的一元线性回归预测值及相应标准估计误差 |
表 1的数据具有随时间明显递增趋势,所以使用SPSS模型中的时间序列建模器来进行ARIMA的拟合与预测[20]。由于数据上升趋势非平稳,为了消除原始数据序列的异方差使数据更为平稳[8],首先进行一阶差分和二阶差分,二阶差分后数据没有明显的上升或下降的趋势,更趋于平稳,因此选定d=2。
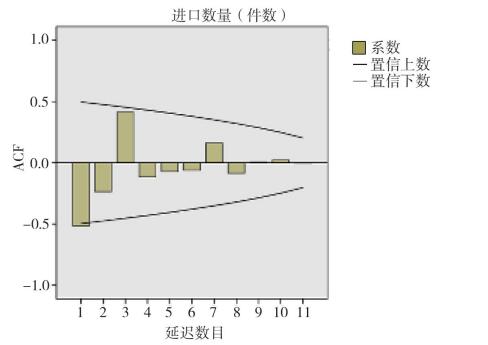
用SPSS作出趋于平稳的自相关函数图(见图 1)和偏自相关函数图(见图 2),可以看出自相关函数图二阶拖尾,偏相关函数三阶拖尾,因此p=2… n和q=3…n,用SPSS把p和q用不同参数值进行组合拟合,最后ARIMA(2, 2, 3)的R2=0.98最接近1,其BIC=15.667最小,因此采用ARIMA(2, 2, 3)进行拟合预测。其预测模型:
| $ \begin{array}{l} {u_t} = 273.867 - 0.933{\mathit{u}_t} - {0.489_{t - 2}} + {\varepsilon _t} + 0.953{\varepsilon _{t - \mathit{1}}} + 0.961{\varepsilon _{t - \mathit{2}}} - \\ \;\;\;\;\;\;0.988{\varepsilon _{t - \mathit{3}}} \end{array} $ |
|
图 1 自相关函数(ACF)图 |
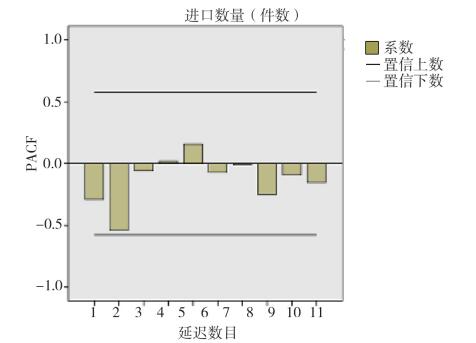
|
图 2 偏自相关函数(PACF)图 |
根据上述建立的预测模型对2001-2015年的检品数量进行摸拟预测,并选择2011-2015年的数据进行预测结果的误差评价,结果见表 3。相比其他3种预测方法,ARIMA模型预测的拟合结果更接近实际数量,并且年度越接近当前,拟合度越高,预测值越准确。
|
|
表 3 4种预测方法的预测结果和相对误差 |
采用ARIMA模型预测2016-2018年的进口检验数量,结果显示:2016年,30544件(30327 ~ 31730件);2017年,32844件(32616 ~ 34097件);2018年,35144件(34905~36465件)。
3 讨论当历史数据随时间呈曲线递增趋势,这种有一定递增规律的数据即可以用时间序列模型进行预测分析。
在对进口检品数量进行预测的4种方法中,考虑单个品种影响因素的一元线性组合预测方法预测出的值接近实际值,该法综合了主要因素的影响,降低了不可靠风险,误差值相对较小,但是会出现个别年份误差较大的现象;而ARIMA(2, 2, 3)方法的拟合度较高,特别对接近当前时间的预测结果的准确度较高。因此,ARIMA方法比其余3种方法具有更高的精确性与可靠性,可以适用于类似本文的数据应用预测。
通过一元线性组合的权重值的大小可以看出,药品A和B所占比重较大,对总检品数量影响较大,这两种检品的递增或递减对总检品有直接影响,药品C也有一定的影响,相较于前两个品种不明显,药品D和E的影响相对较弱。
每种预测方法的预测误差并不是一贯最优或最差,所以任何一种预测模型都存在一定的优劣,要得到更为准确的预测结果,还需要探索非线性组合预测方法,同时考虑国家政策、市场需求等影响因素。
| [1] |
尹志文, 张新平. 浅析《进口药品管理办法》[J]. 中国卫生质量管理, 2004, 11(3): 54-56. |
| [2] |
朱小红. 加强进口药品管理确保进口药品质量[J]. 中国药事, 2003, 17(7): 411-412. |
| [3] |
王子兰, 吴卫中, 祝壮飞, 等. 我国进口药品监督检验制度的研究[J]. 中国药事, 2004, 28(4): 341-343. |
| [4] |
卢日刚, 陈薇, 苏浩, 等. 基于大数据的食品药品检测数据管理系统构建设想[J]. 中国药事, 2016, 30(7): 661-665. |
| [5] |
陈为, 李健胡康. 食品药品检验行业大数据应用探讨[J]. 中国医药导刊, 2014, 16(2): 367-368. |
| [6] |
张琼. 基于三次指数平滑法的建筑主材价格预测[J]. 铁路工程造价管理, 2013(1): 48-51. |
| [7] |
刘红梅, 刘建平. 基于灰色模型的韶山红色旅游景区客源预测[J]. 经济地理, 2010, 30(6): 1047-1051. |
| [8] |
龚国勇. ARIMA模型在深圳GDP预测中的应用[J]. 数学的实践与认识, 2008, 38(4): 53-57. |
| [9] |
杜家龙. 国内生产总值回归预测新探[J]. 统计与决策, 2013(9): 9-14. |
| [10] |
王莎莎, 陈安, 苏静. 组合预测模型在中国GDP预测中的应用[J]. 山东大学学报:理学版, 2009, 44(2): 56-59. |
| [11] |
颜柳, 麻凤海. 三次指数平滑法在城市地铁变形预测中的应用[J]. 交通科技与经济, 2007(5): 62-63, 71. |
| [12] |
陈媛. 应用holt-winters加法模型预测出院人次[J]. 中国卫生统计, 2012, 29(2): 260-261. |
| [13] |
廖峰, 刘清良, 贺辉, 等. 基于改进灰色模型与综合气象因素的母线负荷预测[J]. 电网技术, 2011(10): 183-188. |
| [14] |
蔡辉荣. 一元线性回归模型在厦门航标处航标数量预测中的应用[J]. 中国水运, 2015(4): 76-77. |
| [15] |
许立平, 罗明志. 基于ARIMA模型的黄金价格短期分析预测[J]. 财经科学, 2011(1): 26-34. |
| [16] |
惠春梅. 组合预测模型在物流需求预测及物流体系构建中的应用研究[D]. 昆明: 云南财经大学, 2012.
|
| [17] |
谌小丽, 陈景雅, 王坤. 基于指数平滑法对我国私家车保有量的预测[J]. 华东交通大学学报, 2013(1): 58-63. |
| [18] |
王长江. 指数平滑法中平滑系数的选择研究[J]. 中北大学学报:自然科学版, 2006(6): 558-561. |
| [19] |
蒋昌军. Excel环境下指数平滑预测法最优平滑系数的确定[J]. 中国管理信息化, 2012(2): 13-15. |
| [20] |
刘自强, 王效岳, 白如江. 基于时间序列模型的研究热点分析预测方法研究[J]. 情报理论与实践, 2016, 39(5): 29-33. |
 2017, Vol. 31
2017, Vol. 31 