2. 杭州领业医药科技有限公司, 杭州 310018
2. Quality Unit, Hangzhou SoliPharma Limited Liability Company, Hangzhou, 310018, China
在药品生产企业中,因为种种原因造成供应商变更的情况不在少数,大多数企业认为,做好供应商变更的评估和批准,便能使药品各项检验指标符合质量标准,保证药品质量;然而,对于供应商变更前后药品质量一致性的情况却少有分析和确认。不同供应商供应的原辅料所生产的同一药品,可能都符合药品质量标准,但其药品质量却有着显著性差异。
为了确认供应商变更前后药品质量是否有显著性差异,笔者认为可以采用假设检验的方法。假设检验是数理统计学中根据一定的假设条件,由样本推断总体的一种方法[1-2],在医学、遗传学、气象学以及地理学等领域已有广泛应用,但用于药品生产领域却鲜有报道。笔者使用minitab软件,运用假设检验的方法,采用p值比较法,对一次原料供应商变更前后的药品质量进行显著性差异分析。
1 数据收集公司某药品的含量范围要求为90.0%~100.0%,现公司变更了该药品的原料供应商,收集了10批原料供应商变更后的药品含量数据,并与原料供应商变更前的12批药品含量数据进行比较。其数据见表 1。
|
|
表 1 原料供应商变更前后药品含量 |
在显著性水平α=0.05的条件下,想要确认药品质量是否有显著性差异,属于参数假设检验中的双总体均值检验问题。进行参数假设检验,首先需要确认其数据服从正态分布,且由于原料供应商变更前后药品含量的总体均值μ1和μ2均未知,还需要对原料供应商变更前后药品含量的总体进行方差齐性检验,以确认双总体均值检验采用何种检验方法。
2 方法与分析 2.1 p值比较法所谓p值,指的就是当原假设成立时,出现目前状况的概率[2]。当这个概率很小时,这个结果在原假设成立的条件下就不该在一次试验中出现;但现在它确实出现了,因此有理由认为“原假设成立”的前提是错误的,因而应该拒绝原假设,接受备择假设。由此得到一个最一般的规则:把p值与显著性水平α进行比较,若p值比α小,则拒绝原假设;反之,则不能拒绝原假设[1-4]。
2.2 数据正态性检验使用minitab软件,对原料供应商变更前后的产品含量样本进行正态性检验,得到其样本正态概率图。见图 1、图 2。
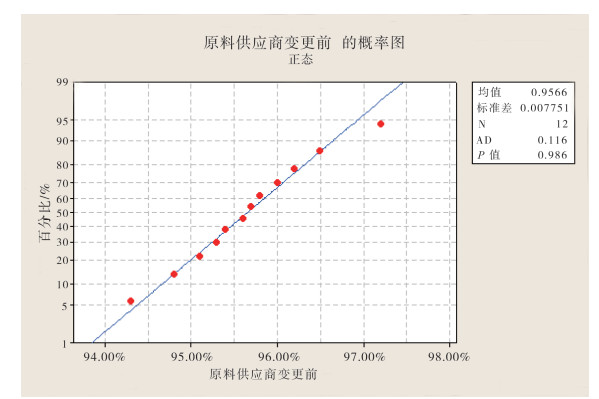
|
图 1 原料供应商变更前药品含量样本正态概率图 |
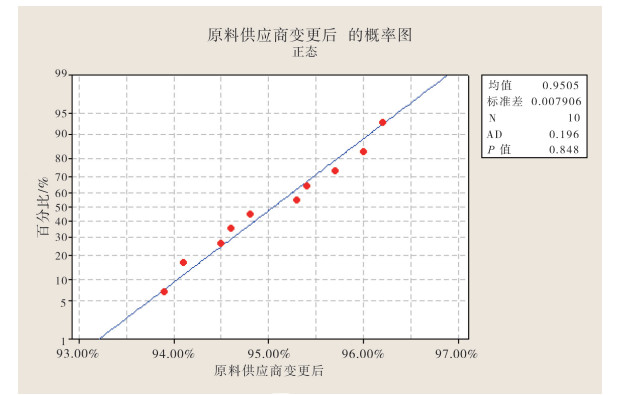
|
图 2 原料供应商变更后药品含量样本正态概率图 |
原料供应商变更前样本正态概率图中p值=0.986;原料供应商变更后样本正态概率图中p值=0.848,虽然原料供应商变更后样本正态概率图中的p值小于原料供应商变更前,但均大于0.05。因此,我们没有足够的证据拒绝原假设,即在当前的情况下,认为两组数据均服从正态分布。
2.3 方差齐性检验方差齐性检验是数理统计学中检查不同样本的总体方差是否相等的一种方法[3-4]。在确认两组数据均服从正态分布的前提下,使用minitab软件,对原料供应商变更前后的药品含量样本进行双总体方差齐性检验,得到的结果见表 2。
|
|
表 2 方差齐性检验结果 |
由于数据服从正态分布,选用F检验,其p值=0.935>0.05,因此,没有足够的证据拒绝原假设,即在当前情况下,认为这两组数据的总体方差是相等的。
2.4 双总体均值检验数据正态性检验确认了原料供应商变更前后的产品含量数据服从正态分布,方差齐性检验确认了两组数据的总体方差相等。因此,对于原料供应商变更前后药品质量是否有显著性差异的双总体均值检验,宜采用t检验方法,其检验功效最高[5-7]。
使用minitab软件,对原料供应商变更前后的药品含量样本进行双总体均值检验,得到的结果见表 3。
|
|
表 3 t检验结果 |
检验中P值=0.084>0.05,因此没有足够的证据拒绝原假设,即在显著性水平α=0.05的条件下,认为原料供应商变更前后,药品质量没有显著性差异。
3 结果通过反复使用数理统计学中的假设检验,首先确认了原料供应商变更前后所抽取的药品含量数据服从正态分布,奠定了后续工作的基础。通过方差齐性检验确认了两组数据的总体方差相等,从而采用t检验对药品质量是否有显著性差异进行假设检验。最后,通过t检验得出结论,认为在显著性水平α=0.05的条件下,原料供应商变更前后的药品质量没有显著性差异。
4 结论由于观测到的样本数据总会带有误差,因此不能简单的由样本统计量结果直接作出判断。使用假设检验的数理统计学方法,可以在不同显著性水平上判断数据的显著性差异,得出科学的结论[6-8]。在药品生产领域,供应商的变更、设备的变更以及工艺参数的调整等,都会对生产过程产生微小的影响,这种影响从样本数据中无法直观地分辨出来。运用数理统计学中假设检验的方法可以有效地分辨这种微小的变化,为药品生产过程中的质量保证提供科学合理的帮助。
| [1] |
马林, 何桢. 六西格玛管理[M]. 北京: 中国人民大学出版社, 2007.
|
| [2] |
马逢时, 周暐, 刘传冰. 六西格玛管理统计指南:MINITAB使用指导[M]. 北京: 中国人民大学出版社, 2012.
|
| [3] |
常微微, 袁慧, 贺连平, 等. 医学论文中定量资料假设检验方法误用分析[J]. 长江大学学报(自然版), 2015, 12(12): 98-100. |
| [4] |
金松玲, 李美花. 医学论文中假设检验的正确应用[J]. 延边大学医学学报, 2005, 28(4): 308-309. |
| [5] |
王平. 假设检验的意义和步骤[J]. 中外健康文摘, 2012, 9(9): 210-211. |
| [6] |
李滢, 张惠卿, 时涛. 参数检验相关问题分析[J]. 泰山医学院学报, 2008, 29(2): 141-142. |
| [7] |
安胜利. 假设检验应用中的常见问题及改进方法[J]. 南方医科大学学报, 2007, 27(3): 382-383. |
| [8] |
祝国强, 黄平, 滕海英, 等. 谈谈假设检验的目的[J]. 数理医药学杂志, 2005, 18(5): 512-513. |
 2017, Vol. 31
2017, Vol. 31 
